Skip to contents

Imperfect serological test

Source: vignettes/imperfect_test.Rmd
imperfect_test.Rmd
library(serosv)
library(ggplot2)
#> Warning: package 'ggplot2' was built under R version 4.3.3

Imperfect test

Function correct_prevalence() is used for estimating the true prevalence if the serological test used is imperfect

Arguments:

  • data the input data frame, must either have:

    • age, pos, tot columns (for aggregated data)

    • OR age, status columns for (linelisting data)

  • bayesian whether to adjust sero-prevalence using the Bayesian or frequentist approach. If set to TRUE, true sero-prevalence is estimated using MCMC.

  • init_se sensitivity of the serological test (default value 0.95)

  • init_sp specificity of the serological test (default value 0.8)

  • study_size_se (applicable when bayesian=TRUE) sample size for sensitivity validation study (default value 1000)

  • study_size_sp (applicable when bayesian=TRUE) sample size for specificity validation study (default value 1000)

  • chains (applicable when bayesian=TRUE) number of Markov chains (default to 1)

  • warmup (applicable when bayesian=TRUE) number of warm up runs (default value 1000)

  • iter (applicable when bayesian=TRUE) number of iterations (default value 2000)

The function will return a list of 2 items:

  • info

    • if bayesian = TRUE contains estimated values for se, sp and corrected seroprevalence

    • else return the formula for computing corrected seroprevalence

  • corrected_sero return a data.frame with age, sero (corrected sero) and pos, tot (adjusted based on corrected prevalence)

# ---- estimate real prevalence using Bayesian approach ----
data <- rubella_uk_1986_1987
output <- correct_prevalence(data, warmup = 1000, iter = 4000, init_se=0.9, init_sp = 0.8, study_size_se=1000, study_size_sp=3000)
#> 
#> SAMPLING FOR MODEL 'prevalence_correction' NOW (CHAIN 1).
#> Chain 1: 
#> Chain 1: Gradient evaluation took 9.6e-05 seconds
#> Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.96 seconds.
#> Chain 1: Adjust your expectations accordingly!
#> Chain 1: 
#> Chain 1: 
#> Chain 1: Iteration:    1 / 4000 [  0%]  (Warmup)
#> Chain 1: Iteration:  400 / 4000 [ 10%]  (Warmup)
#> Chain 1: Iteration:  800 / 4000 [ 20%]  (Warmup)
#> Chain 1: Iteration: 1001 / 4000 [ 25%]  (Sampling)
#> Chain 1: Iteration: 1400 / 4000 [ 35%]  (Sampling)
#> Chain 1: Iteration: 1800 / 4000 [ 45%]  (Sampling)
#> Chain 1: Iteration: 2200 / 4000 [ 55%]  (Sampling)
#> Chain 1: Iteration: 2600 / 4000 [ 65%]  (Sampling)
#> Chain 1: Iteration: 3000 / 4000 [ 75%]  (Sampling)
#> Chain 1: Iteration: 3400 / 4000 [ 85%]  (Sampling)
#> Chain 1: Iteration: 3800 / 4000 [ 95%]  (Sampling)
#> Chain 1: Iteration: 4000 / 4000 [100%]  (Sampling)
#> Chain 1: 
#> Chain 1:  Elapsed Time: 2.026 seconds (Warm-up)
#> Chain 1:                4.044 seconds (Sampling)
#> Chain 1:                6.07 seconds (Total)
#> Chain 1:

# check fitted value 
output$info[1:2, ]
#>             mean      se_mean          sd      2.5%       25%       50%
#> est_se 0.9278179 0.0001098350 0.006095913 0.9151759 0.9239329 0.9279511
#> est_sp 0.8028005 0.0001011728 0.006973970 0.7888135 0.7981642 0.8028934
#>              75%     97.5%    n_eff      Rhat
#> est_se 0.9318726 0.9390499 3080.323 0.9998417
#> est_sp 0.8075049 0.8167427 4751.518 0.9996668

# ---- estimate real prevalence using frequentist approach ----
freq_output <- correct_prevalence(data, bayesian = FALSE, init_se=0.9, init_sp = 0.8)

# check info
freq_output$info
#> [1] "Formula: real_sero = (observed_sero + sp - 1) / (se + sp -1)"

User can then visualize the output using plot_corrected_prev() function

# Plot output of the frequentist approach
plot_corrected_prev(freq_output)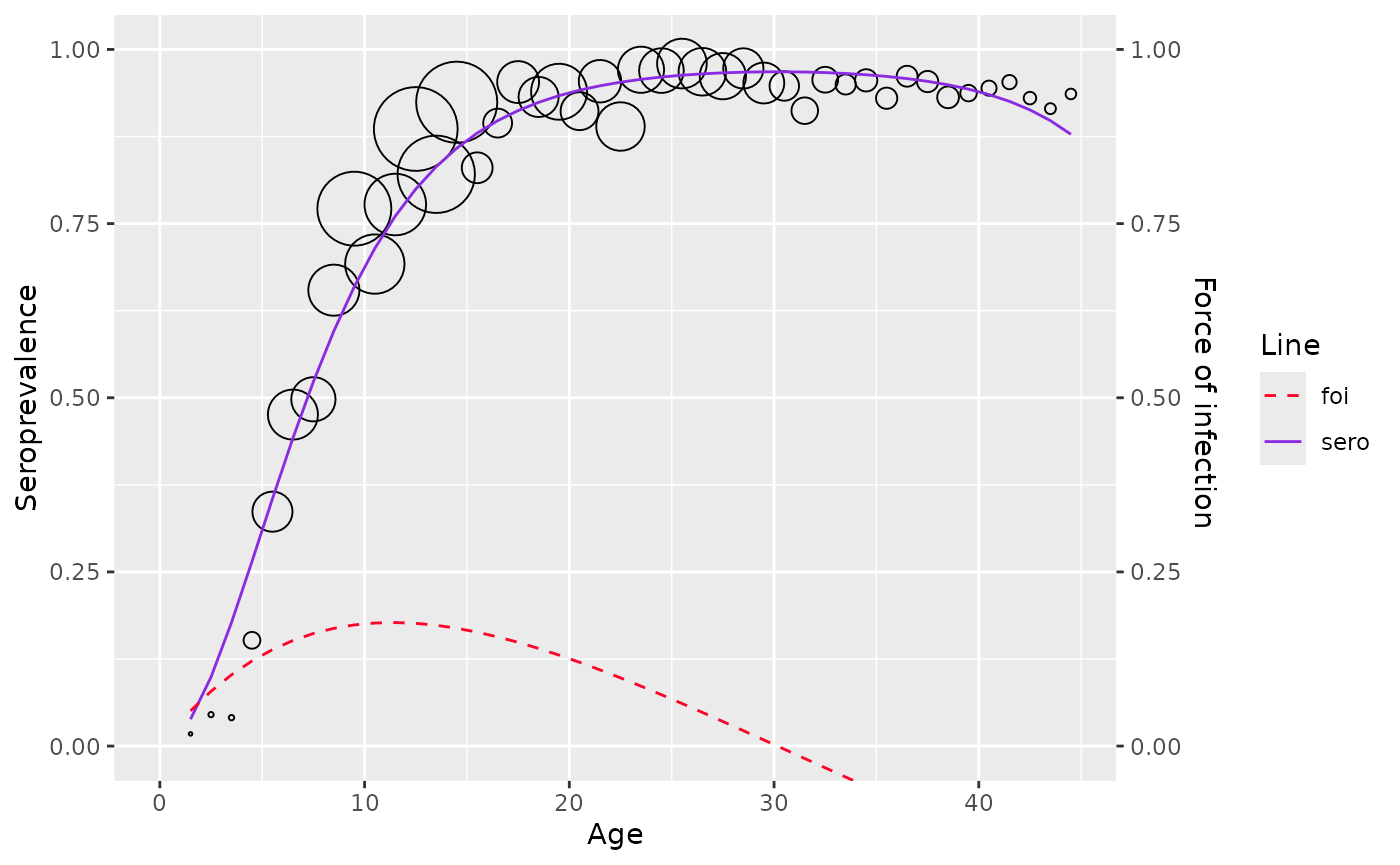


# Plot output of the bayesian approach 
plot_corrected_prev(output)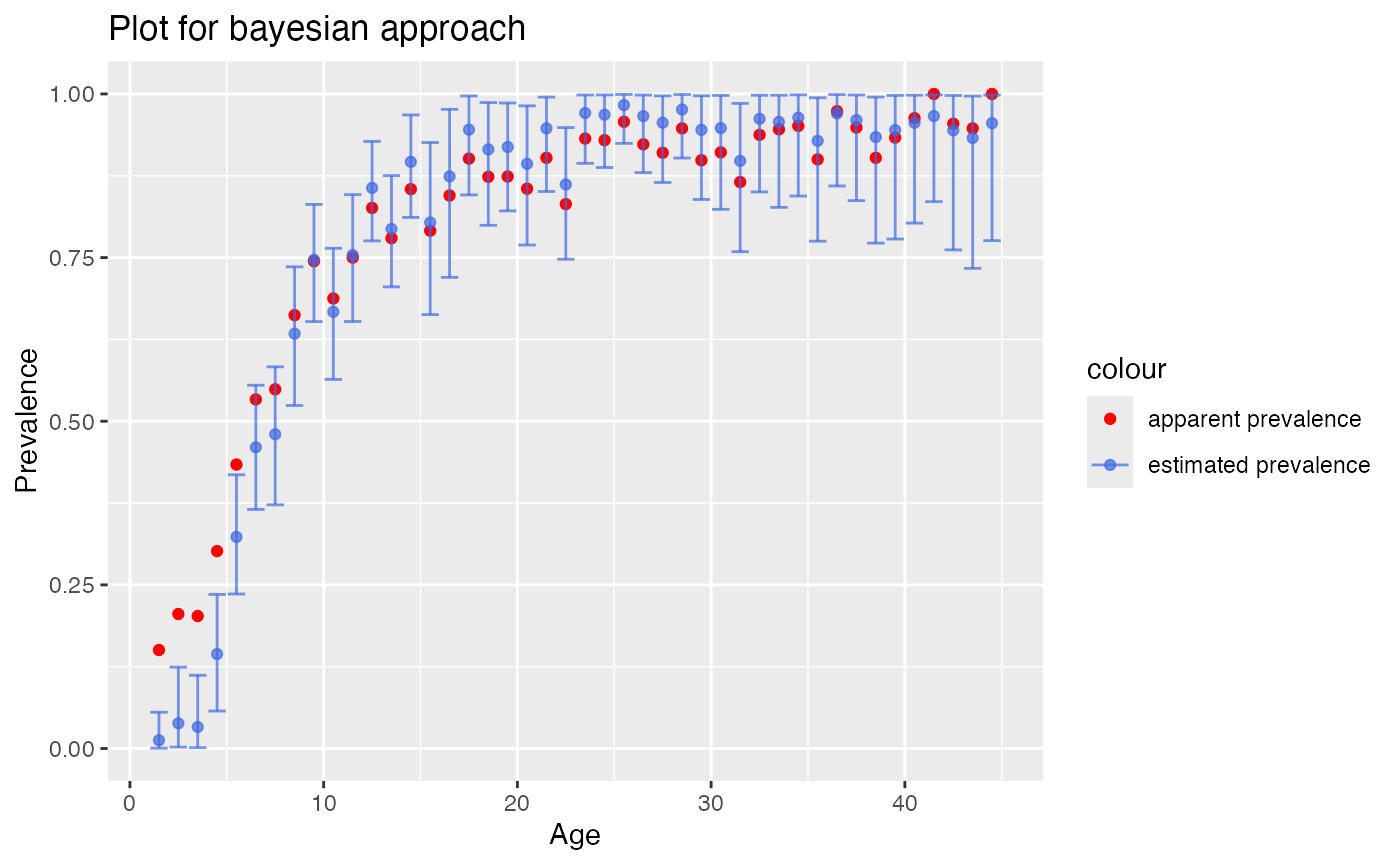

To compare both correction methods in a single plot, provide the output from the second method as the optional y argument in plot_corrected_prev()

plot_corrected_prev(output, freq_output)


# set facet = TRUE to display the confidence or credible intervals for each method
plot_corrected_prev(output, freq_output, facet = TRUE)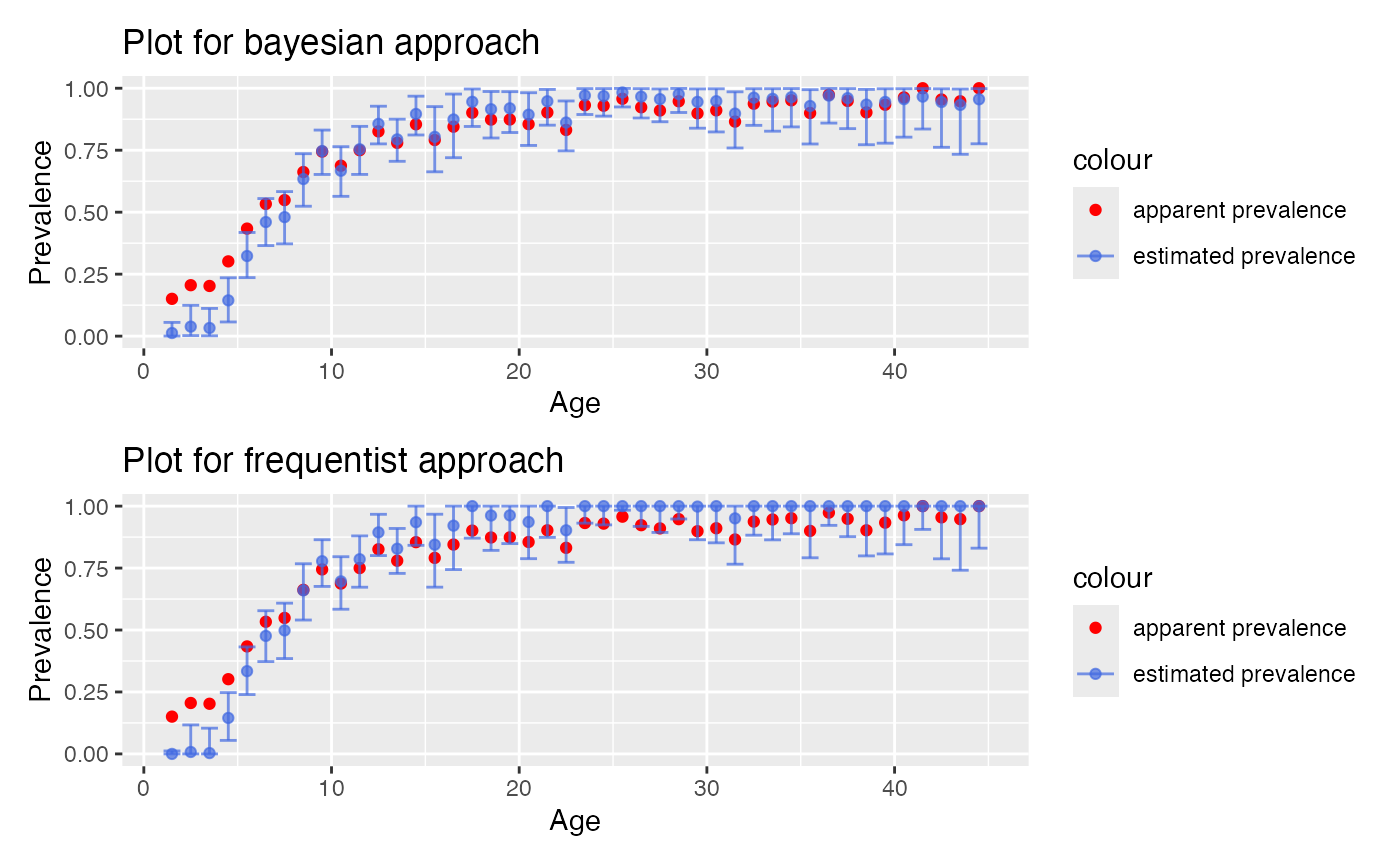

Fitting corrected data

Data after seroprevalence correction

Bayesian approach

suppressWarnings(
  corrected_data <- farrington_model(
  output$corrected_se,
  start=list(alpha=0.07,beta=0.1,gamma=0.03))
)

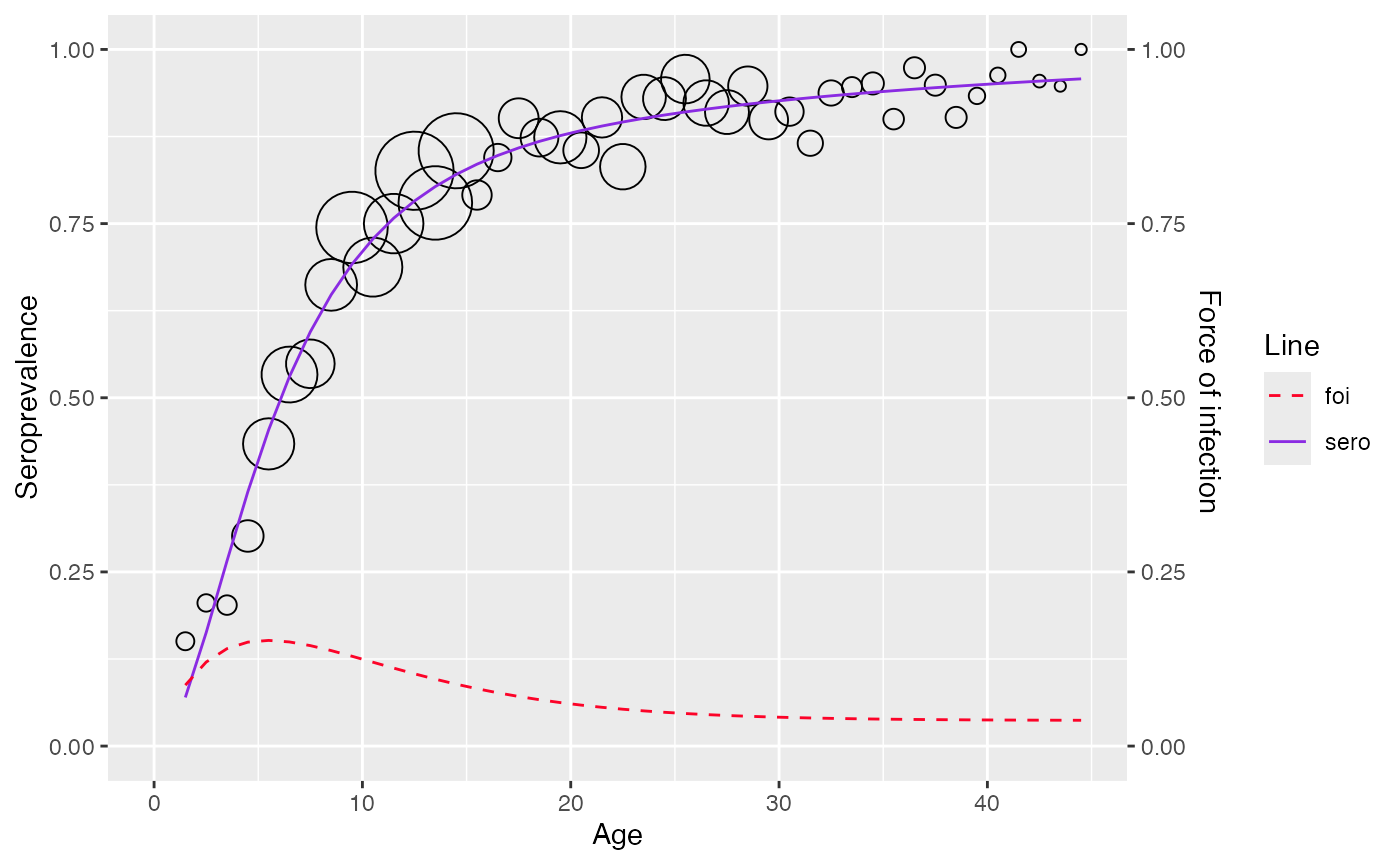
plot(corrected_data)
#> Warning: No shared levels found between `names(values)` of the manual scale and the
#> data's fill values.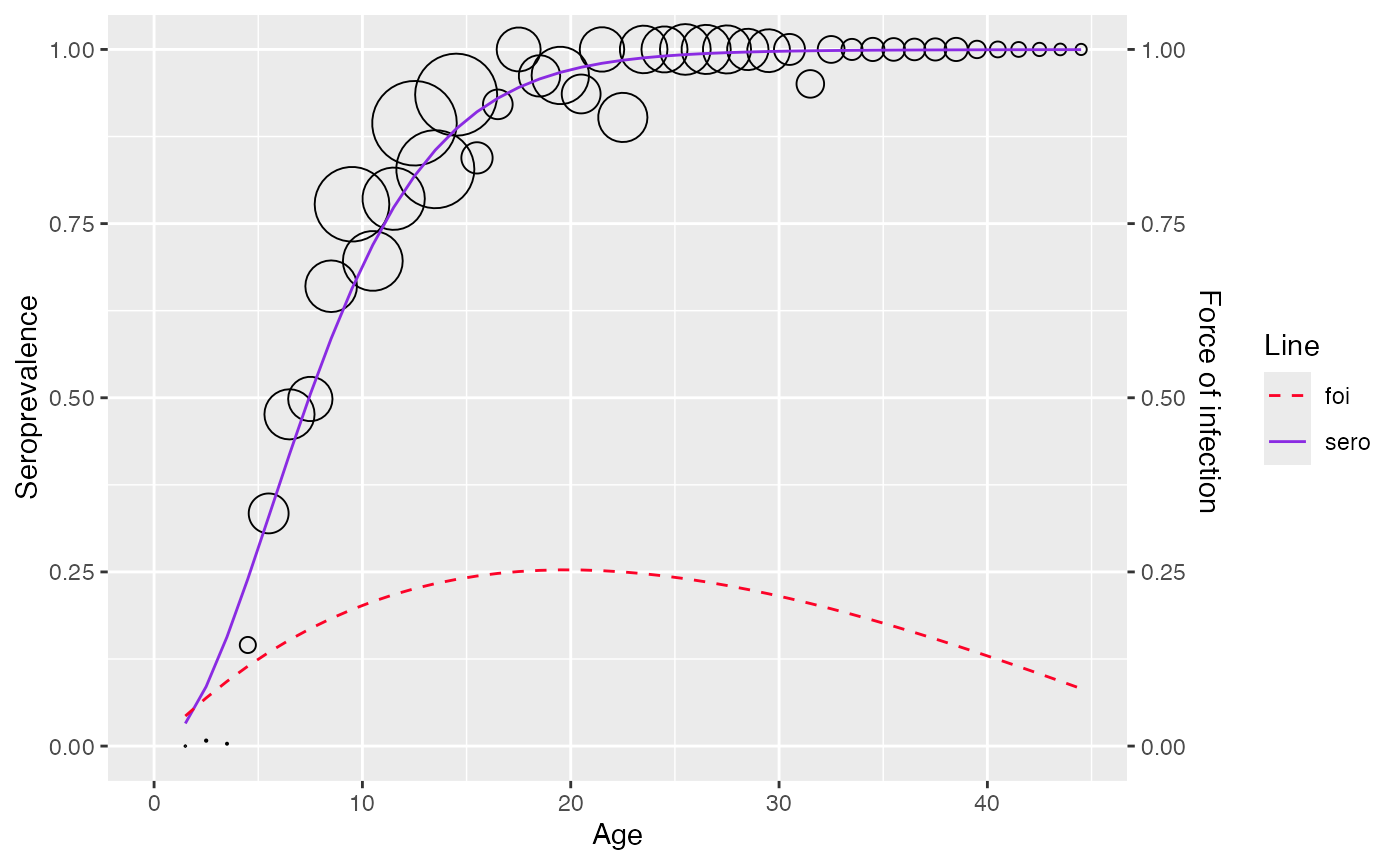

Frequentist approach

suppressWarnings(
  corrected_data <- farrington_model(
  freq_output$corrected_se,
  start=list(alpha=0.07,beta=0.1,gamma=0.03))
)

plot(corrected_data)
#> Warning: No shared levels found between `names(values)` of the manual scale and the
#> data's fill values.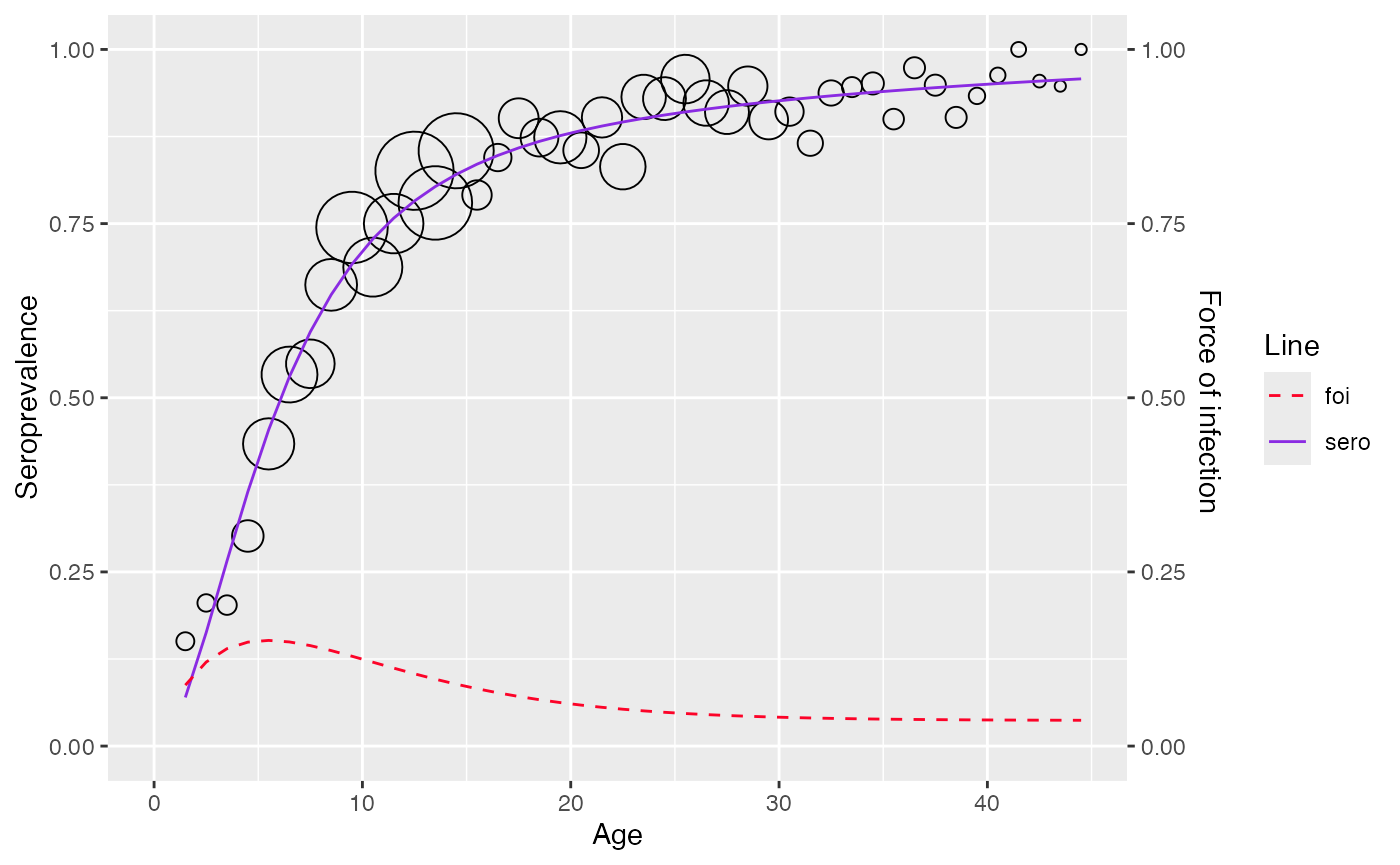

Original data

suppressWarnings(
  original_data <- farrington_model(
  data,
  start=list(alpha=0.07,beta=0.1,gamma=0.03))
)
plot(original_data)
#> Warning: No shared levels found between `names(values)` of the manual scale and the
#> data's fill values.