Skip to contents

Nonparametric model

Source: vignettes/nonparametric_model.Rmd
nonparametric_model.Rmd

Local estimation by polynomial

Refer to Chapter 7.1

Proposed model

Within the local polynomial framework, the linear predictor \(\eta(a)\) is approximated locally at one particular value \(a_0\) for age by a line (local linear) or a parabola (local quadratic).

The estimator for the \(k\)-th derivative of \(\eta(a_0)\), for \(k = 0,1,…,p\) (degree of local polynomial) is as followed:

\[ \hat{\eta}^{(k)}(a_0) = k!\hat{\beta}_k(a_0) \]

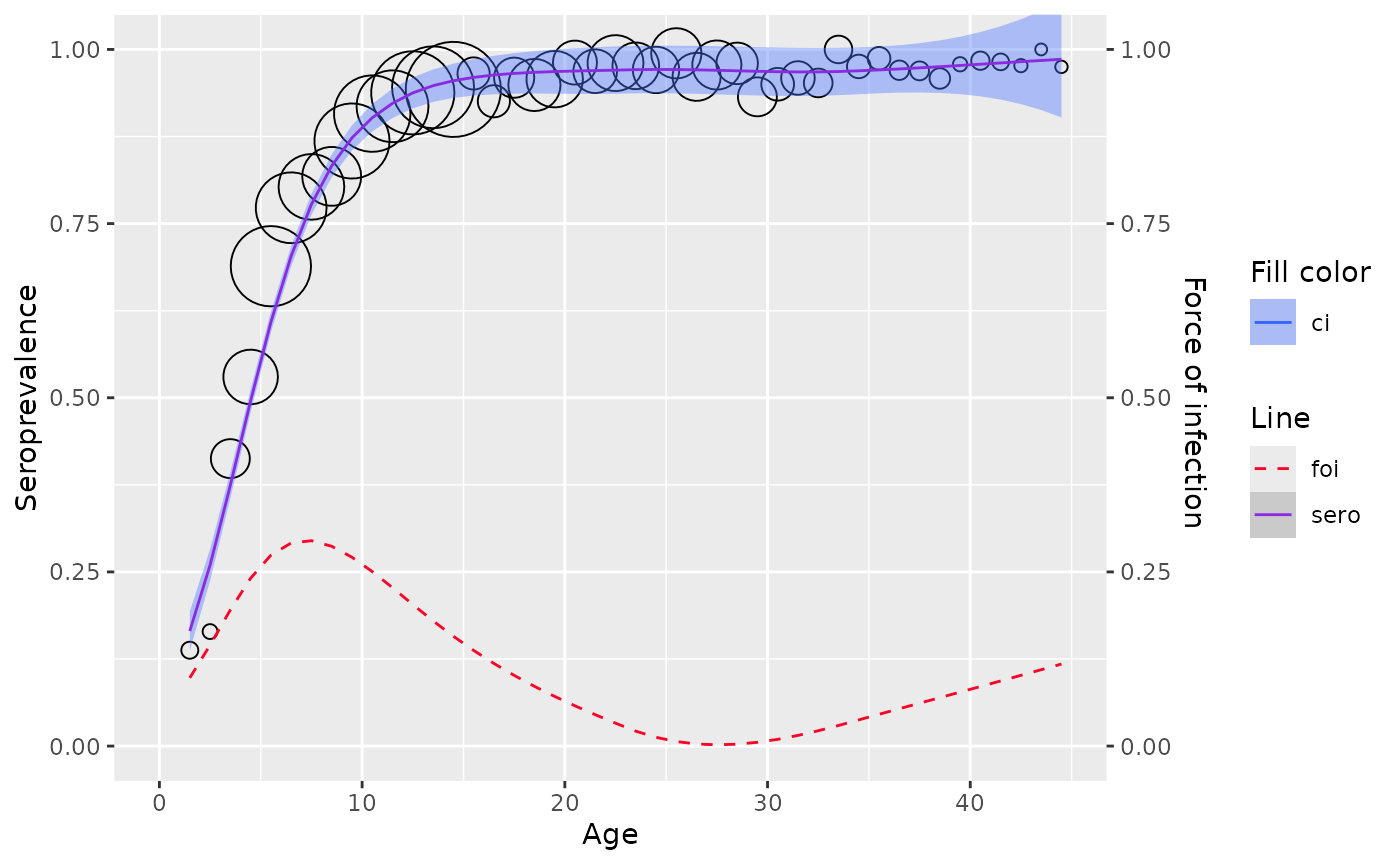
The estimator for the prevalence at age \(a_0\) is then given by

\[ \hat{\pi}(a_0) = g^{-1}\{ \hat{\beta}_0(a_0) \} \]

  • Where \(g\) is the link function

The estimator for the force of infection at age \(a_0\) by assuming \(p \ge 1\) is as followed

\[ \hat{\lambda}(a_0) = \hat{\beta}_1(a_0) \delta \{ \hat{\beta}_0 (a_0) \} \]

  • Where \(\delta \{ \hat{\beta}_0(a_0) \} = \frac{dg^{-1} \{ \hat{\beta}_0(a_0) \} } {d\hat{\beta}_0(a_0)}\)

Fitting data

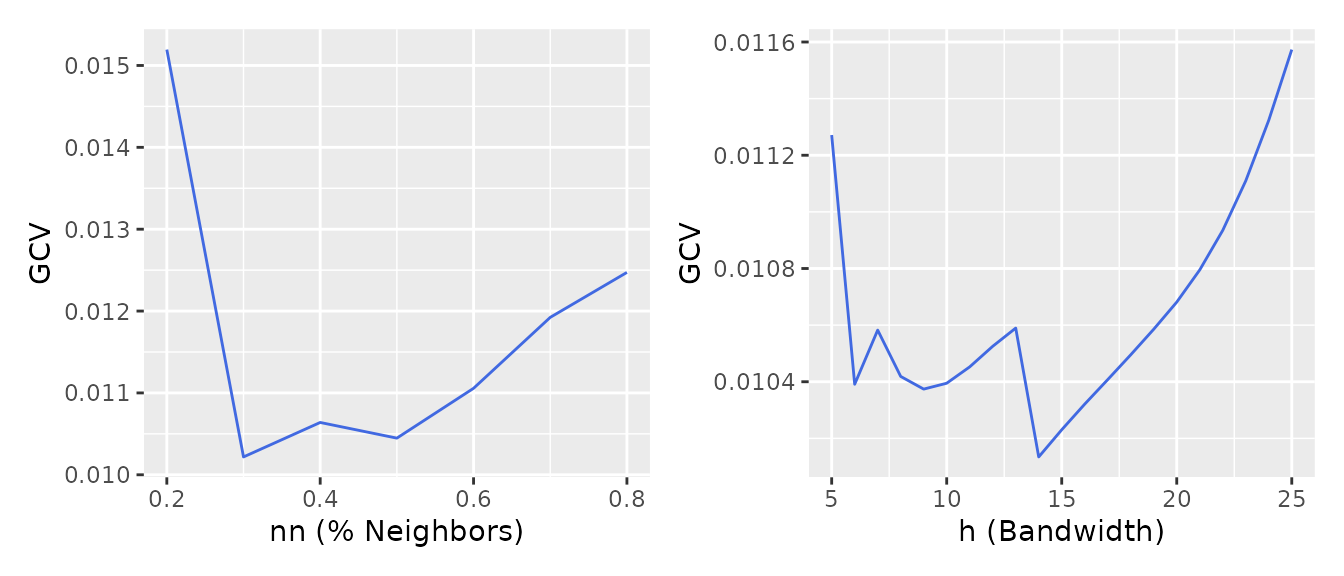
mump <- mumps_uk_1986_1987
age <- mump$age
pos <- mump$pos
tot <- mump$tot
y <- pos/tot

Use plot_gcv() to show GCV curves for the nearest neighbor method (left) and constant bandwidth (right).

plot_gcv(
   age, pos, tot,
   nn_seq = seq(0.2, 0.8, by=0.1),
   h_seq = seq(5, 25, by=1)
 )

Use lp_model() to fit a local estimation by polynomials.

lp <- lp_model(age, pos = pos, tot = tot, kern="tcub", nn=0.7, deg=2)
plot(lp)