Skip to contents

Parametric models

Source: vignettes/parametric_model.Rmd
parametric_model.Rmd

Polynomial models

Refer to Chapter 6.1.1

Use polynomial_model() to fit a polynomial model.

We will use the Hepatitis A data from Belgium 1993–1994 for this example.

a <- hav_bg_1964
neg <- a$tot -a$pos
pos <- a$pos
age <- a$age
tot <- a$tot

Muench model

Proposed model

(Muench 1934) suggested to model the infection process with so-called “catalytic model”, in which the distribution of the time spent in the susceptible class in SIR model is exponential with rate β\beta

π(a)=k(1−e−βa) \pi(a) = k(1 - e^{-\beta a} )

Where:

  • π\pi is the seroprevalence at age aa

  • 1−k1 - k is the proportion of population that stay uninfected for a lifetime

  • aa is the variable age

Under this catalytic model and assuming that k=1k = 1, force infection would be λ(a)=β\lambda(a) = \beta

Fitting data

Muench’s model can be estimated by either defining k = 1 (a degree one linear predictor, note that it is irrelevant to the k in the proposed model) or setting the type = "Muench".

muench1 <- polynomial_model(age, pos = pos, tot = tot, k = 1)
summary(muench1$info)
#> 
#> Call:
#> glm(formula = age(k), family = binomial(link = link), data = df)
#> 
#> Coefficients:
#>      Estimate Std. Error z value Pr(>|z|)    
#> Age -0.050500   0.002457  -20.55   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance:    Inf  on 83  degrees of freedom
#> Residual deviance: 97.275  on 82  degrees of freedom
#> AIC: 219.19
#> 
#> Number of Fisher Scoring iterations: 5

muench2 <- polynomial_model(age, pos = pos, tot = tot, type = "Muench")
summary(muench2$info)
#> 
#> Call:
#> glm(formula = age(k), family = binomial(link = link), data = df)
#> 
#> Coefficients:
#>      Estimate Std. Error z value Pr(>|z|)    
#> Age -0.050500   0.002457  -20.55   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance:    Inf  on 83  degrees of freedom
#> Residual deviance: 97.275  on 82  degrees of freedom
#> AIC: 219.19
#> 
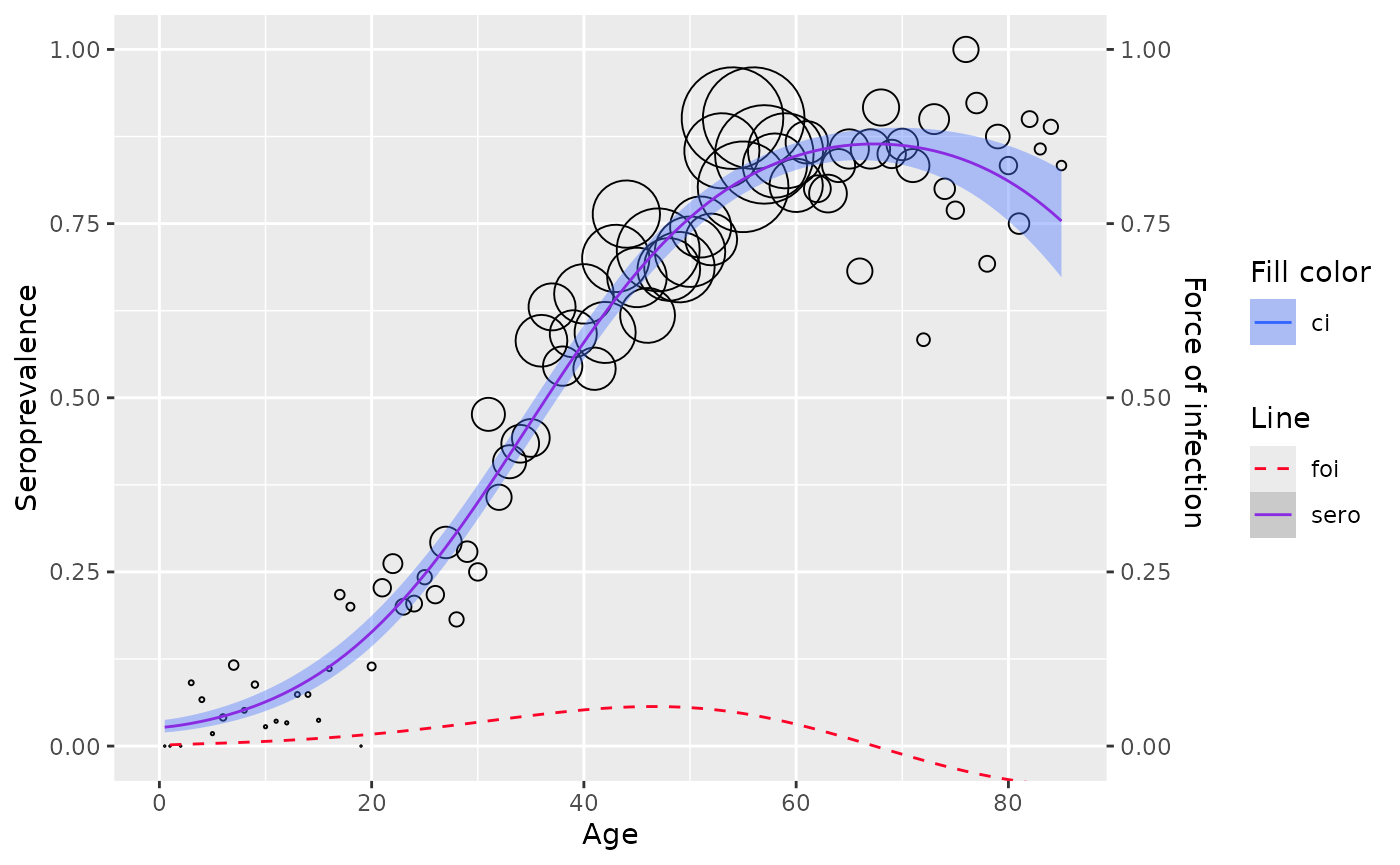
#> Number of Fisher Scoring iterations: 5

We can plot any model with the plot() function.

plot(muench2)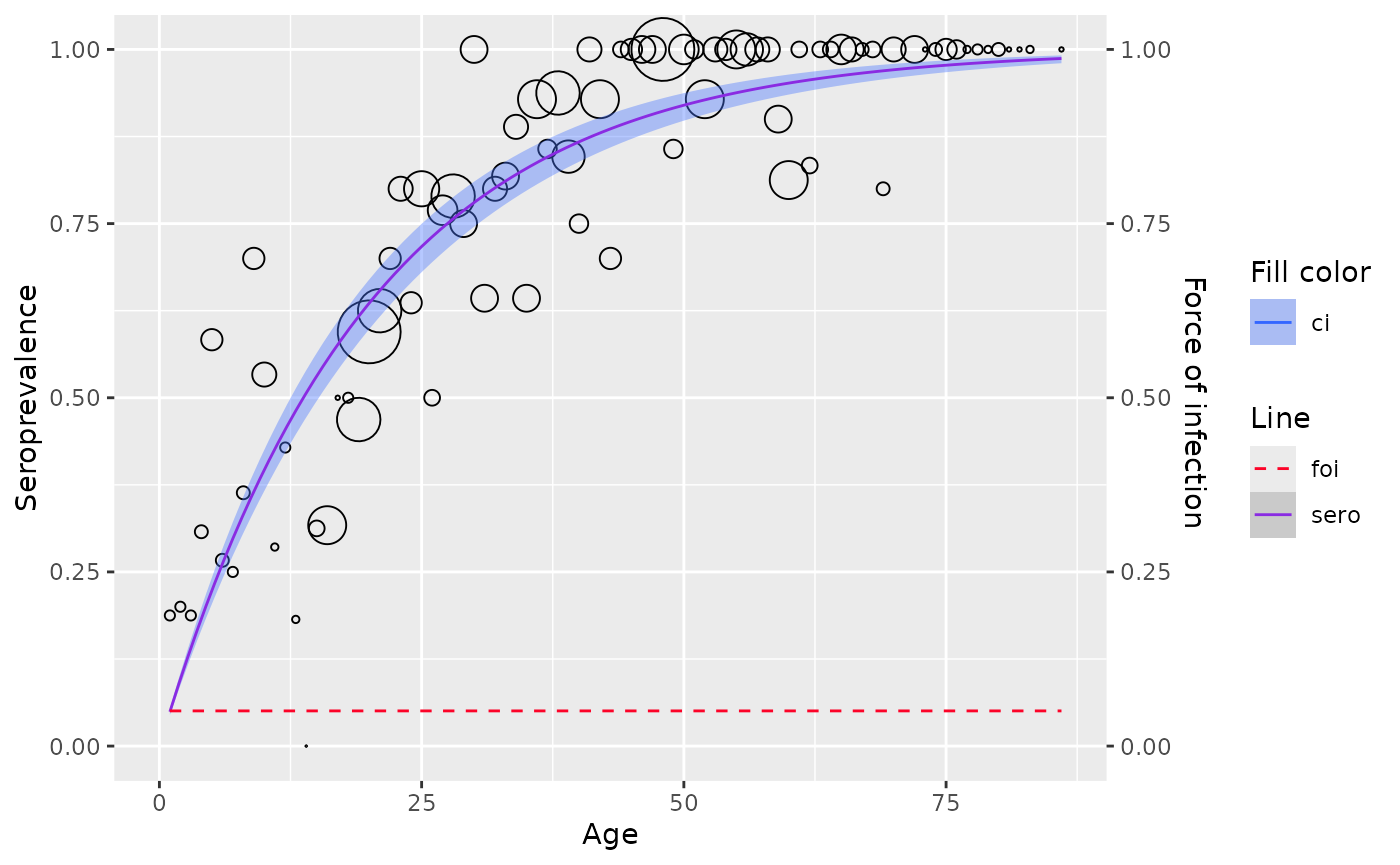

Griffith model

Proposed model

Griffith proposed a model for force of infection as followed

λ(a)=β1+2β2a \lambda(a) = \beta_1 + 2\beta_2a

Which can be estimated using a GLM where the for which the linear predictor was η(a)=β1+β2a2\eta(a) = \beta_1 + \beta_2a^{2}

Fitting data

Similarly, we can estimate Griffith’s model either by defining k = 2, or setting the type = "Griffith"

gf_model <- polynomial_model(age, pos = pos, tot = tot, type = "Griffith")
plot(gf_model)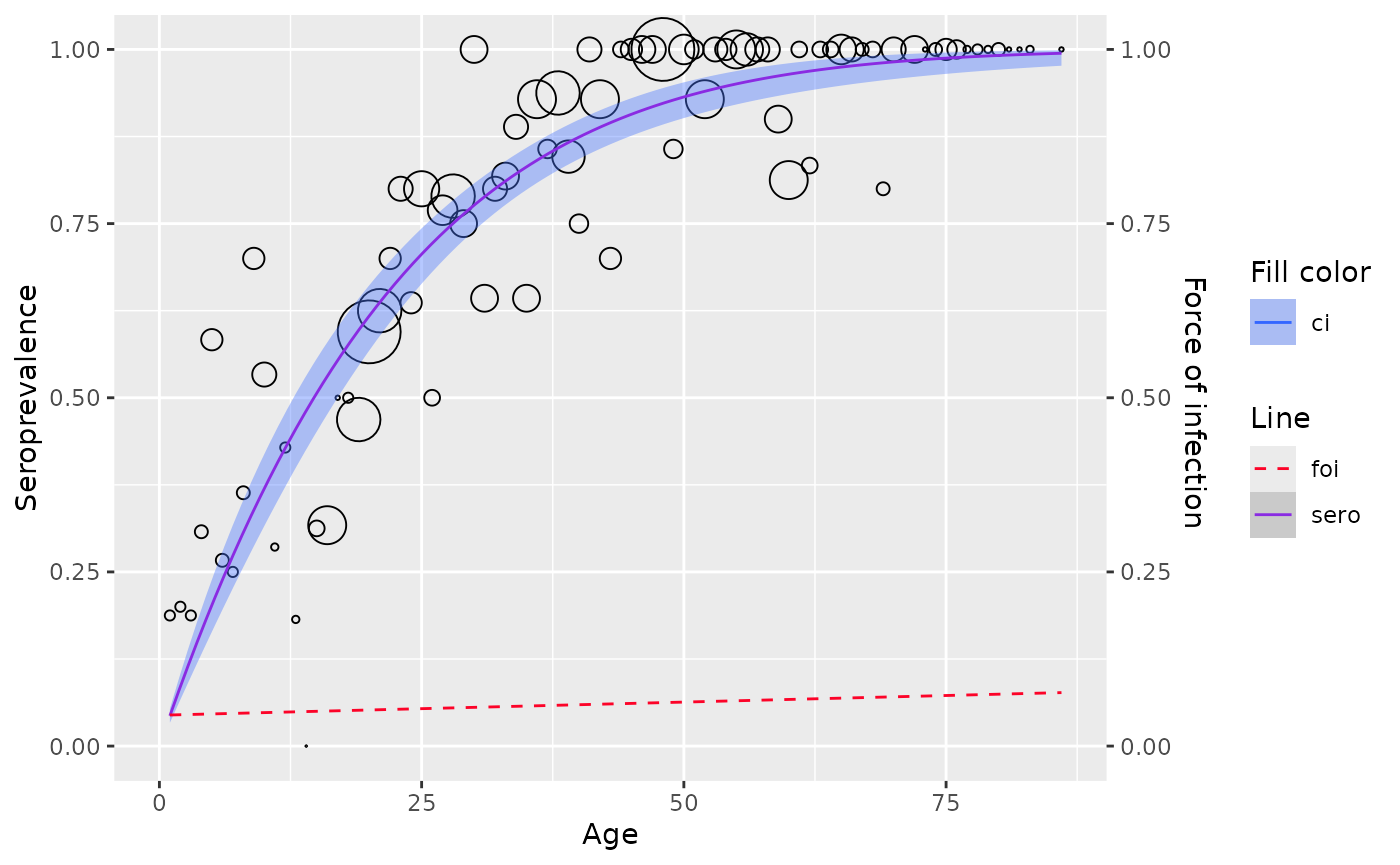

Grenfell and Anderson model

Proposed model

(Grenfell and Anderson 1985) extended the models of Muench and Griffiths further suggest the use of higher order polynomial functions to model the force of infection which assumes prevalence model as followed

π(a)=1−e−Σiβiai \pi(a) = 1 - e^{-\Sigma_i \beta_i a^i}

Which implies that force of infection equals λ(a)=Σβiiai−1\lambda(a) = \Sigma \beta_i i a^{i-1}

Fitting data

And Grenfell and Anderson’s model.

grf_model <- polynomial_model(age, pos = pos, tot = tot, type = "Grenfell")
plot(grf_model)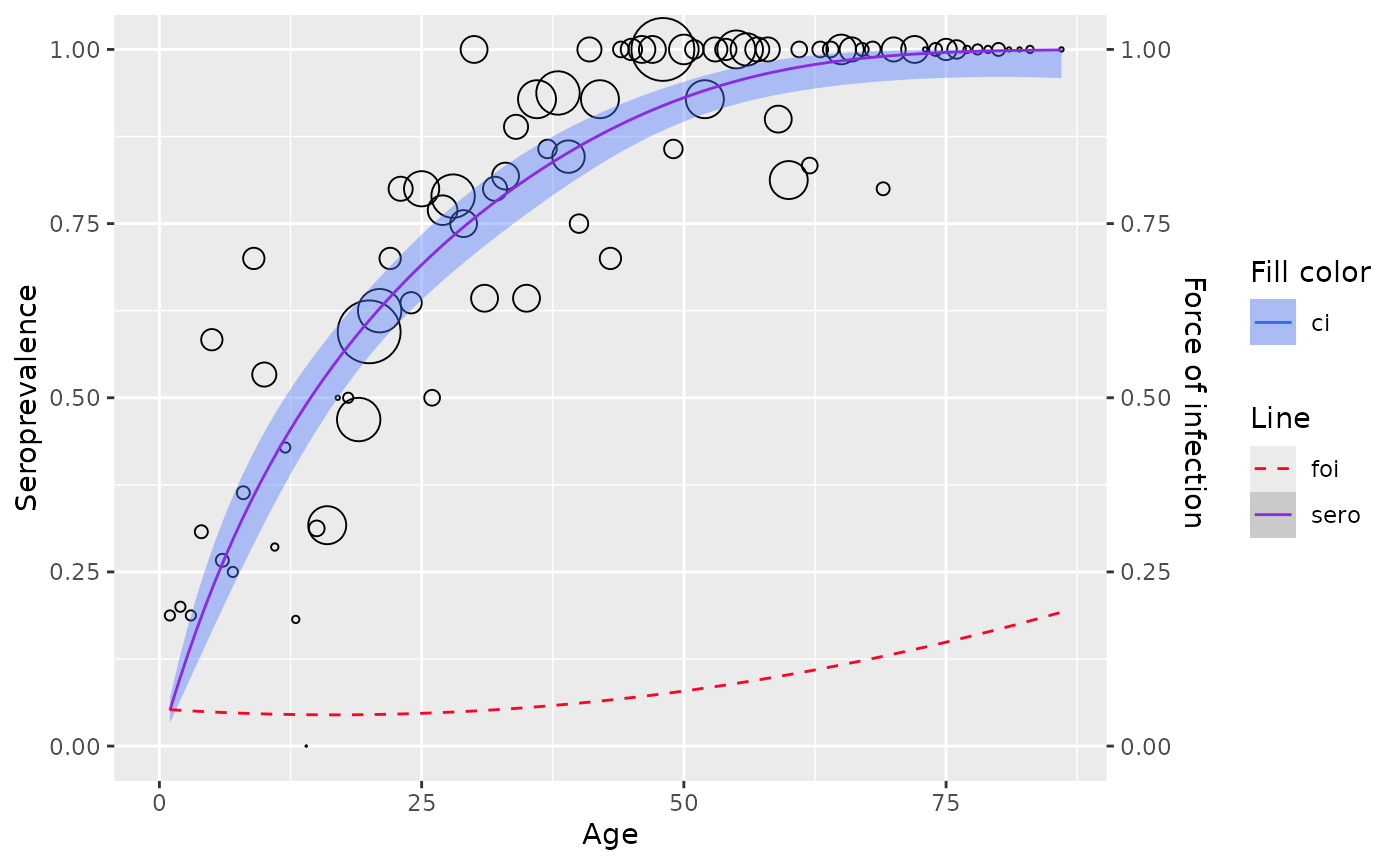

Nonlinear models

Refer to Chapter 6.1.2

Farrington model

Proposed model

For Farrington’s model, the force of infection was defined non-negative for all a λ(a)≥0\lambda(a) \geq 0 and increases to a peak in a linear fashion followed by an exponential decrease

λ(a)=(αa−γ)e−βa+γ \lambda(a) = (\alpha a - \gamma)e^{-\beta a} + \gamma

Where γ\gamma is called the long term residual for FOI, as a→∞a \rightarrow \infty , λ(a)→γ\lambda (a) \rightarrow \gamma

Integrating λ(a)\lambda(a) would results in the following non-linear model for prevalence

$$ \pi (a) = 1 - e^{-\int_0^a \lambda(s) ds} \\ = 1 - exp\{ \frac{\alpha}{\beta}ae^{-\beta a} + \frac{1}{\beta}(\frac{\alpha}{\beta} - \gamma)(e^{-\beta a} - 1) -\gamma a \} $$

Fitting data

Use farrington_model() to fit a Farrington’s model.

rubella <- rubella_uk_1986_1987
rubella$neg <- rubella$tot - rubella$pos

farrington_md <- farrington_model(
   rubella$age, pos = rubella$pos, tot = rubella$tot,
   start=list(alpha=0.07,beta=0.1,gamma=0.03)
   )
plot(farrington_md)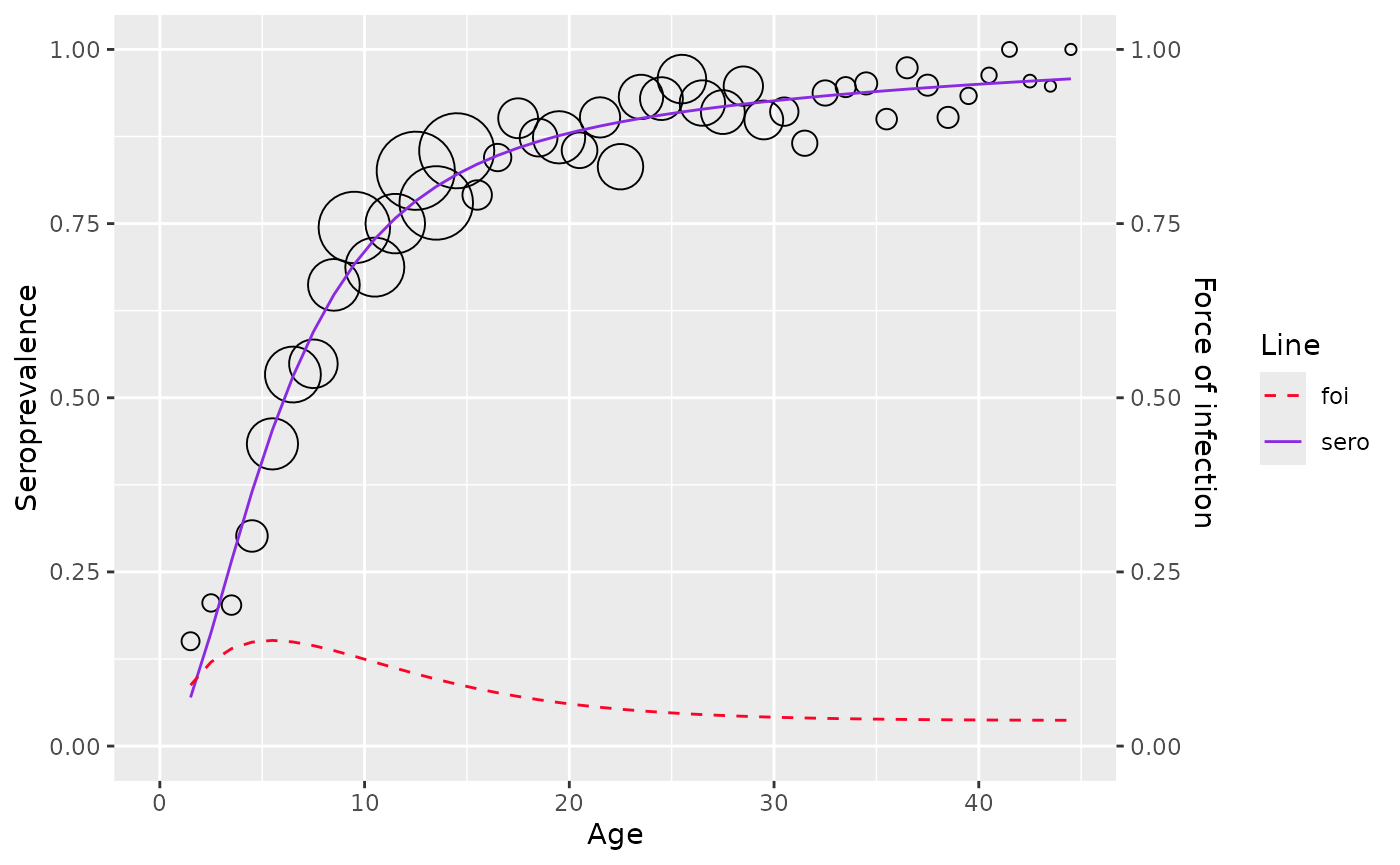

Weibull model

Proposed model

For a Weibull model, the prevalence is given by

π(d)=1−e−β0dβ1 \pi (d) = 1 - e^{ - \beta_0 d ^ {\beta_1}}

Where dd is exposure time (difference between age of injection and age at test)

The model was reformulated as a GLM model with log - log link and linear predictor using log(d)

η(d)=log(β0)+β1log(d)\eta(d) = log(\beta_0) + \beta_1 log(d)

Thus implies that the force of infection is a monotone function of the exposure time as followed

λ(d)=β0β1dβ1−1 \lambda(d) = \beta_0 \beta_1 d^{\beta_1 - 1}

Fitting data

Use weibull_model() to fit a Weibull model.

hcv <- hcv_be_2006[order(hcv_be_2006$dur), ]
dur <- hcv$dur
infected <- hcv$seropositive

wb_md <- weibull_model(
   t = dur,
   status = infected
   )
plot(wb_md)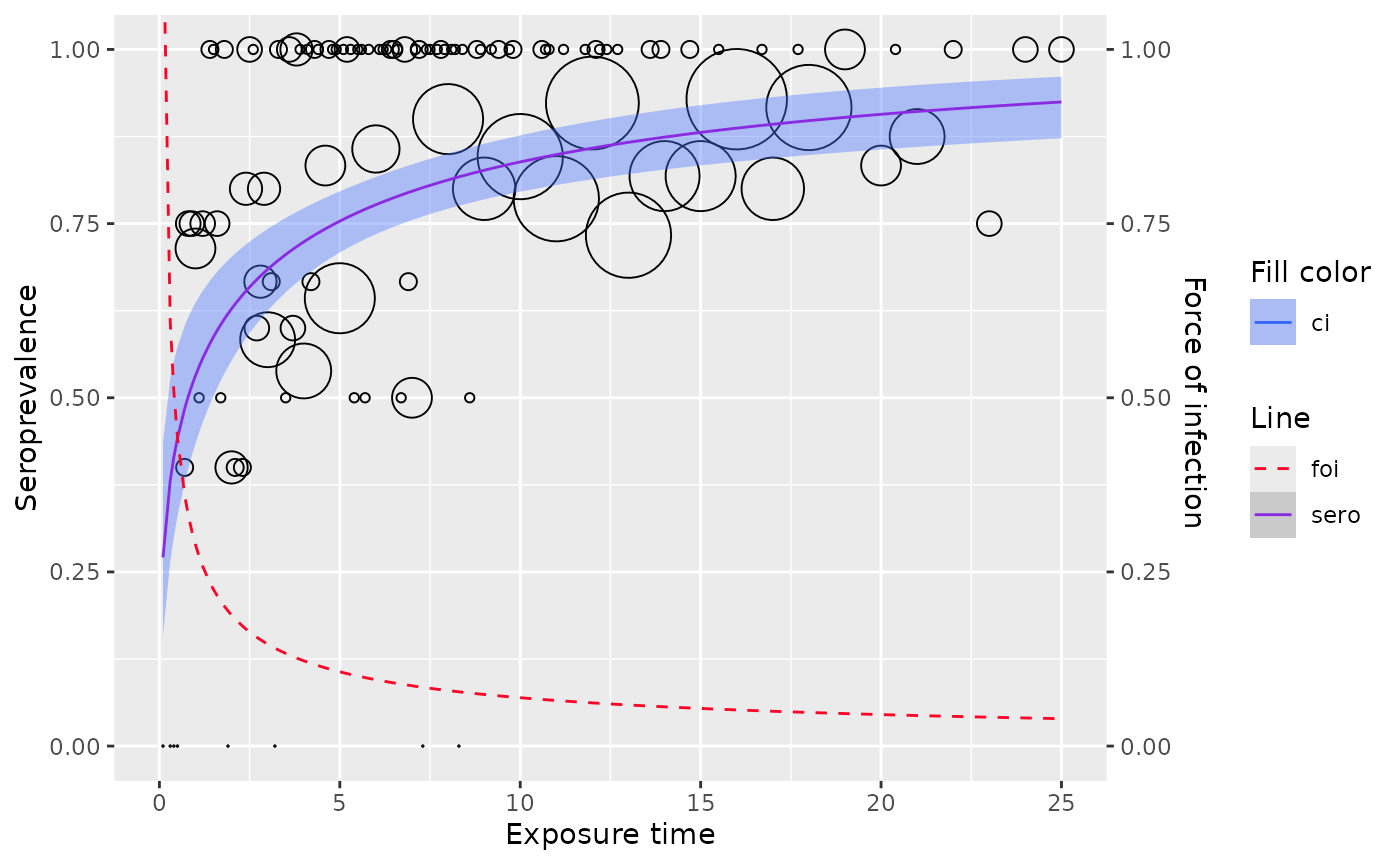

Fractional polynomial model

Refer to Chapter 6.2

Proposed model

Fractional polynomial model generalize conventional polynomial class of functions. In the context of binary responses, a fractional polynomial of degree mm for the linear predictor is defined as followed

ηm(a,β,p1,p2,...,pm)=Σi=0mβiHi(a) \eta_m(a, \beta, p_1, p_2, ...,p_m) = \Sigma^m_{i=0} \beta_i H_i(a)

Where mm is an integer, p1≤p2≤...≤pmp_1 \le p_2 \le... \le p_m is a sequence of powers, and Hi(a)H_i(a) is a transformation given by

Hi={api if pi≠pi−1,Hi−1(a)×log(a) if pi=pi−1, H_i = \begin{cases} a^{p_i} & \text{ if } p_i \neq p_{i-1}, \\ H_{i-1}(a) \times log(a) & \text{ if } p_i = p_{i-1}, \end{cases}

Best power selection

Use find_best_fp_powers() to find the powers which gives the lowest deviance score

hav <- hav_be_1993_1994
best_p <- find_best_fp_powers(
  hav$age, pos = hav$pos,tot = hav$tot,
  p=seq(-2,3,0.1), mc=FALSE, degree=2, link="cloglog"
)
best_p
#> $p
#> [1] 1.5 1.6
#> 
#> $deviance
#> [1] 81.60333
#> 
#> $model
#> 
#> Call:  glm(formula = as.formula(formulate(p_cur)), family = binomial(link = link))
#> 
#> Coefficients:
#> (Intercept)   I(age^1.5)   I(age^1.6)  
#>    -3.61083      0.12443     -0.07656  
#> 
#> Degrees of Freedom: 85 Total (i.e. Null);  83 Residual
#> Null Deviance:       1320 
#> Residual Deviance: 81.6  AIC: 361.2

Fitting data

Use fp_model() to fit a fractional polynomial model

model <- fp_model(
  hav$age, pos = hav$pos, tot = hav$tot,
  p=c(1.5, 1.6), link="cloglog")
compute_ci.fp_model(model)
#>             x          y       ymin       ymax
#> 1    0.500000 0.02716482 0.01959292 0.03760634
#> 2    1.353535 0.02862007 0.02076739 0.03938180
#> 3    2.207071 0.03050022 0.02229336 0.04166326
#> 4    3.060606 0.03272353 0.02411019 0.04434334
#> 5    3.914141 0.03526829 0.02620530 0.04738857
#> 6    4.767677 0.03813303 0.02858256 0.05079025
#> 7    5.621212 0.04132595 0.03125392 0.05455127
#> 8    6.474747 0.04486080 0.03423621 0.05868100
#> 9    7.328283 0.04875493 0.03754957 0.06319273
#> 10   8.181818 0.05302816 0.04121663 0.06810243
#> 11   9.035354 0.05770215 0.04526197 0.07342778
#> 12   9.888889 0.06279986 0.04971170 0.07918768
#> 13  10.742424 0.06834517 0.05459314 0.08540179
#> 14  11.595960 0.07436252 0.05993448 0.09209011
#> 15  12.449495 0.08087661 0.06576446 0.09927268
#> 16  13.303030 0.08791198 0.07211204 0.10696929
#> 17  14.156566 0.09549275 0.07900598 0.11519909
#> 18  15.010101 0.10364218 0.08647445 0.12398036
#> 19  15.863636 0.11238230 0.09454458 0.13333012
#> 20  16.717172 0.12173352 0.10324196 0.14326387
#> 21  17.570707 0.13171416 0.11259010 0.15379519
#> 22  18.424242 0.14234005 0.12260991 0.16493547
#> 23  19.277778 0.15362405 0.13331910 0.17669357
#> 24  20.131313 0.16557562 0.14473160 0.18907544
#> 25  20.984848 0.17820037 0.15685696 0.20208387
#> 26  21.838384 0.19149963 0.16969980 0.21571816
#> 27  22.691919 0.20547006 0.18325928 0.22997380
#> 28  23.545455 0.22010329 0.19752856 0.24484227
#> 29  24.398990 0.23538562 0.21249445 0.26031074
#> 30  25.252525 0.25129778 0.22813709 0.27636190
#> 31  26.106061 0.26781475 0.24442970 0.29297378
#> 32  26.959596 0.28490571 0.26133858 0.31011961
#> 33  27.813131 0.30253403 0.27882315 0.32776771
#> 34  28.666667 0.32065739 0.29683627 0.34588144
#> 35  29.520202 0.33922801 0.31532461 0.36441921
#> 36  30.373737 0.35819301 0.33422931 0.38333451
#> 37  31.227273 0.37749480 0.35348672 0.40257603
#> 38  32.080808 0.39707168 0.37302931 0.42208783
#> 39  32.934343 0.41685844 0.39278668 0.44180970
#> 40  33.787879 0.43678713 0.41268659 0.46167752
#> 41  34.641414 0.45678779 0.43265608 0.48162384
#> 42  35.494949 0.47678937 0.45262248 0.50157854
#> 43  36.348485 0.49672055 0.47251437 0.52146971
#> 44  37.202020 0.51651067 0.49226246 0.54122460
#> 45  38.055556 0.53609057 0.51180028 0.56077069
#> 46  38.909091 0.55539345 0.53106484 0.58003679
#> 47  39.762626 0.57435568 0.54999703 0.59895424
#> 48  40.616162 0.59291745 0.56854205 0.61745792
#> 49  41.469697 0.61102348 0.58664964 0.63548732
#> 50  42.323232 0.62862347 0.60427423 0.65298738
#> 51  43.176768 0.64567252 0.62137511 0.66990917
#> 52  44.030303 0.66213145 0.63791643 0.68621046
#> 53  44.883838 0.67796694 0.65386716 0.70185598
#> 54  45.737374 0.69315156 0.66920108 0.71681762
#> 55  46.590909 0.70766374 0.68389659 0.73107434
#> 56  47.444444 0.72148757 0.69793657 0.74461197
#> 57  48.297980 0.73461254 0.71130813 0.75742291
#> 58  49.151515 0.74703320 0.72400232 0.76950564
#> 59  50.005051 0.75874875 0.73601383 0.78086420
#> 60  50.858586 0.76976255 0.74734066 0.79150759
#> 61  51.712121 0.78008167 0.75798364 0.80144916
#> 62  52.565657 0.78971633 0.76794612 0.81070592
#> 63  53.419192 0.79867939 0.77723350 0.81929794
#> 64  54.272727 0.80698582 0.78585282 0.82724767
#> 65  55.126263 0.81465218 0.79381235 0.83457942
#> 66  55.979798 0.82169617 0.80112116 0.84131869
#> 67  56.833333 0.82813613 0.80778876 0.84749172
#> 68  57.686869 0.83399062 0.81382480 0.85312499
#> 69  58.540404 0.83927809 0.81923866 0.85824471
#> 70  59.393939 0.84401643 0.82403928 0.86287648
#> 71  60.247475 0.84822275 0.82823488 0.86704484
#> 72  61.101010 0.85191307 0.83183279 0.87077301
#> 73  61.954545 0.85510205 0.83483926 0.87408252
#> 74  62.808081 0.85780288 0.83725937 0.87699300
#> 75  63.661616 0.86002700 0.83909685 0.87952200
#> 76  64.515152 0.86178403 0.84035397 0.88168483
#> 77  65.368687 0.86308166 0.84103143 0.88349447
#> 78  66.222222 0.86392548 0.84112821 0.88496159
#> 79  67.075758 0.86431902 0.84064144 0.88609456
#> 80  67.929293 0.86426362 0.83956628 0.88689948
#> 81  68.782828 0.86375845 0.83789584 0.88738031
#> 82  69.636364 0.86280045 0.83562110 0.88753895
#> 83  70.489899 0.86138442 0.83273093 0.88737534
#> 84  71.343434 0.85950298 0.82921209 0.88688755
#> 85  72.196970 0.85714665 0.82504940 0.88607189
#> 86  73.050505 0.85430394 0.82022587 0.88492295
#> 87  73.904040 0.85096143 0.81472299 0.88343368
#> 88  74.757576 0.84710393 0.80852105 0.88159545
#> 89  75.611111 0.84271461 0.80159953 0.87939813
#> 90  76.464646 0.83777525 0.79393761 0.87683008
#> 91  77.318182 0.83226642 0.78551469 0.87387829
#> 92  78.171717 0.82616781 0.77631105 0.87052838
#> 93  79.025253 0.81945855 0.76630847 0.86676475
#> 94  79.878788 0.81211754 0.75549100 0.86257063
#> 95  80.732323 0.80412392 0.74384571 0.85792827
#> 96  81.585859 0.79545748 0.73136344 0.85281900
#> 97  82.439394 0.78609923 0.71803967 0.84722350
#> 98  83.292929 0.77603184 0.70387518 0.84112196
#> 99  84.146465 0.76524031 0.68887688 0.83449431
#> 100 85.000000 0.75371250 0.67305839 0.82732055
plot(model)

Grenfell, B. T., and R. M. Anderson. 1985. “The Estimation of Age-Related Rates of Infection from Case Notifications and Serological Data.” The Journal of Hygiene 95 (2): 419–36. https://doi.org/10.1017/s0022172400062859.
Muench, Hugo. 1934. “Derivation of Rates from Summation Data by the Catalytic Curve.” Journal of the American Statistical Association 29 (185): 25–38. https://doi.org/10.1080/01621459.1934.10502684.